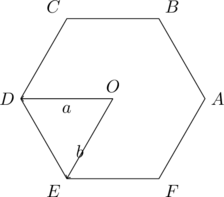
题目:如图,正六边形 \(ABCDEF\),连接 \(OE\)、\(OD\),如果 \(\overrightarrow{OD} = \vec{a}\),\(\overrightarrow{OE} = \vec{b}\),那么 \(\overrightarrow{AB} = \_\_\_\_\_\_\_\_\_\_\).
详细解答
- 正六边形的性质分析
正六边形的每个内角为120°,各边长度相等,中心O到各顶点的距离相等。已知\(\overrightarrow{OD} = \vec{a}\),\(\overrightarrow{OE} = \vec{b}\),需通过向量运算求\(\overrightarrow{AB}\)。 - 关键步骤解析
- 连接BD:由正六边形对称性可知,\(AB = DE\),且\(\angle ABD = \angle BDE = 90^\circ\),因此\(AB \parallel DE\)。
- 向量关系:因为\(AB \parallel DE\)且长度相等,故\(\overrightarrow{AB} = \overrightarrow{ED}\)。
- 向量减法:\(\overrightarrow{ED}\)表示从E到D的位移,即\(\overrightarrow{ED} = \overrightarrow{OD} – \overrightarrow{OE} = \vec{a} – \vec{b}\)。
- 结论
\(\overrightarrow{AB} = \vec{a} – \vec{b}\)。
相关知识点复习
- 正六边形的性质
- 所有边长相等,内角均为120°。
- 中心到各顶点的距离相等,对角线具有对称性。
- 向量的运算
- 向量减法:\(\overrightarrow{ED} = \overrightarrow{OD} – \overrightarrow{OE}\),表示从E到D的位移。
- 平行向量:若两向量方向相同、长度相等,则它们相等(如\(\overrightarrow{AB} = \overrightarrow{ED}\))。
- 几何推理
- 利用平行线的判定(同位角、内错角相等)证明线段平行。
- 通过对称性简化问题(如正六边形中边的对称关系)。
易错与常错点
- 向量方向混淆
- 错误:将\(\overrightarrow{ED}\)写成\(\overrightarrow{DE}\)(即\(\overrightarrow{OE} – \overrightarrow{OD}\))。
- 正确:\(\overrightarrow{ED} = \overrightarrow{OD} – \overrightarrow{OE}\)。
- 几何关系误判
- 错误:认为AB与DE不平行,导致无法建立向量关系。
- 正确:通过角度计算(如90°)证明AB与DE平行。
- 符号错误
- 错误:将答案写为\(\vec{b} – \vec{a}\),忽略向量方向。
- 正确:严格按照位移方向计算(从E到D为\(\vec{a} – \vec{b}\))。
答案
\(\boxed{\vec{a} – \vec{b}}\)
