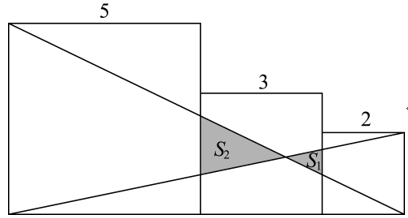
17. 如图 5,边长分别为 5,3,2 的三个正方形拼接在一起,它们的一边在同一直线上,那么图中阴影三角形①和②的面积之比 \(\frac{S_1}{S_2}\) 的比值为______
详细解答:
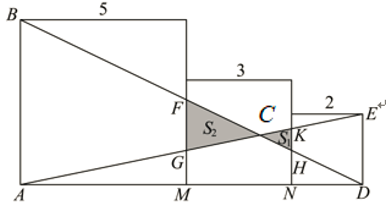
根据题意,得 \(AM = 5\),\(AN = 8\),\(AD = 10\),\(DE = 2\),\(AB \parallel FG \parallel KH \parallel DE\)。
因为 \(AB \parallel DE\),所以 \(\triangle ABC \sim \triangle EDC\),因此 \(\frac{AC}{EC} = \frac{AB}{DE} = \frac{5}{2}\)。
由此可得 \(AC = \frac{5}{7}AE\),\(CE = \frac{2}{7}AE\)。
因为 \(MG \parallel DE\),所以 \(\frac{AG}{AE} = \frac{AM}{AD} = \frac{1}{2}\),因此 \(AG = \frac{1}{2}AE\)。
同理可得 \(AK = \frac{4}{5}AE\)。
于是 \(CG = AC – AG = \frac{3}{14}AE\),\(CK = AK – AC = \frac{3}{35}AE\)。
因此 \(\frac{CG}{CK} = \frac{\frac{3}{14}AE}{\frac{3}{35}AE} = \frac{5}{2}\)。
因为 \(FG \parallel KH\),所以 \(\triangle CKH \sim \triangle CGF\)。
所以 \(\frac{S_1}{S_2} = \left(\frac{CK}{CG}\right)^2 = \left(\frac{2}{5}\right)^2 = \frac{4}{25}\)。
故答案为:\(\frac{4}{25}\)。
相关知识点复习:
- 相似三角形的判定与性质:如果两个三角形的对应角相等,对应边成比例,则这两个三角形相似。相似三角形的对应边成比例,对应高的比等于相似比,对应周长的比等于相似比,对应面积的比等于相似比的平方。
- 平行线分线段成比例定理:两条直线被一组平行线所截,所得的对应线段成比例。
易错提示和拓展:
- 在解题过程中,要注意正确识别相似三角形,并利用相似比进行计算。
- 注意区分不同线段的比例关系,避免混淆。
- 拓展:可以进一步探讨不同形状的图形拼接后形成的复杂图形的面积计算问题。
