几何题目:正方形中的相似三角形
题目
正方形 ![]() 的边长为 1,点
的边长为 1,点 ![]() 在
在 ![]() 的延长线上,且
的延长线上,且 ![]() 。延长
。延长 ![]() 、
、![]() ,如果
,如果 ![]() ,求
,求 ![]() 。(如图 3 所示)
。(如图 3 所示)
图形
以下是正方形 ![]() 、点
、点 ![]() 及延长线
及延长线 ![]() 、
、![]() 的示意图:
的示意图:
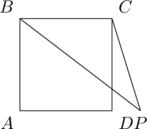
解答
已知条件:正方形 ![]() ,边长
,边长 ![]() 。点
。点 ![]() 在
在 ![]() 的延长线上,且
的延长线上,且 ![]() ,即
,即 ![]() 。设
。设 ![]() ,其中
,其中 ![]() 。
。![]() ,求
,求 ![]() 。
。
我们给各点赋坐标:![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点 ![]() ,其中
,其中 ![]() ,所以
,所以 ![]() .
.
步骤 1:利用相似三角形:由于 ![]() ,对应角为
,对应角为 ![]() ,
,![]() ,
,![]() 。对应边为
。对应边为 ![]() ,
,![]() ,
,![]() 。所以有比例关系:
。所以有比例关系:
![]()
其中 ![]() ,
,![]() ,
,![]() ,
,![]() 。代入得:
。代入得:
![]()
解得:
![]()
![]()
取正根:![]() ,满足
,满足 ![]() 。所以
。所以 ![]() .
.
步骤 2:计算 ![]() :我们计算
:我们计算 ![]() 中
中 ![]() 。使用坐标几何方法:
。使用坐标几何方法:
- 向量
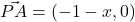
- 向量
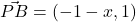
直线 ![]() 的斜率
的斜率 ![]() ,直线
,直线 ![]() 的斜率
的斜率 ![]() 。所以:
。所以:
![Rendered by QuickLaTeX.com \[ \tan \angle BPA = \left| \frac{m_1 - m_2}{1 + m_1 m_2} \right| = \left| \frac{0 - \frac{1}{-1-x}}{1} \right| = \frac{1}{1+x} \]](https://tilearn.space/wp-content/ql-cache/quicklatex.com-8c3f86d6506f3c105ca112aeb956f758_l3.png)
代入 ![]() :
:
![]()
![]()
有理化分母:
![]()
答:![]() 。
。![]()
小结
通过这个问题,我们学习了如何利用相似三角形的性质求解几何问题。同学们可以尝试改变 ![]() 的值,探索
的值,探索 ![]() 的变化规律,进一步加深对相似三角形的理解!
的变化规律,进一步加深对相似三角形的理解!
