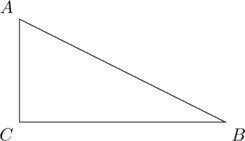
6. 如图1,![]() 中,
中,![]() ,
, ![]() ,
, ![]() 。如果以点
。如果以点![]() 为圆心,半径为
为圆心,半径为![]() 的⊙
的⊙![]() 与线段
与线段![]() 有两个交点,那么⊙
有两个交点,那么⊙![]() 的半径
的半径![]() 的取值范围是( )
的取值范围是( )
(A) ![]() ;
;
(B) ![]() ;
;
(C) ![]() ;
;
(D) ![]() .
.
题目解析
首先,我们来复习一下相关的知识点:
- 直角三角形的性质:在直角三角形中,斜边是最长的边,且满足勾股定理:
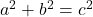 ,其中
,其中 为斜边。
为斜边。 - 正切函数:
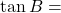 对边/邻边 ,这里指的是在直角三角形中,角
对边/邻边 ,这里指的是在直角三角形中,角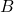 的对边与邻边的比值。
的对边与邻边的比值。 - 圆与直线的关系:当圆与直线相切时,圆心到直线的距离等于圆的半径;当圆与直线相交时,圆心到直线的距离小于圆的半径。
题目要求我们求出以点C为圆心,半径为R的⊙C与线段AB有两个交点时,半径R的取值范围。
首先,我们需要明确几个关键点:
- △ABC是一个直角三角形,其中∠C=90°。
- 已知AB=5,且
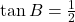 。
。 - 以点C为圆心,半径为R的⊙C与线段AB有两个交点。
根据直角三角形的性质,我们可以得到以下信息:
- 在直角三角形中,斜边是最长的边,因此AC和BC分别是两条直角边。
- 根据勾股定理,有
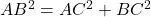 。
。 - 已知AB=5,所以有
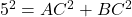 ,即
,即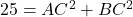 。
。 - 又因为
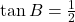 ,所以有
,所以有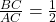 ,即
,即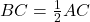 。
。
将![]() 代入到勾股定理中,得到:
代入到勾股定理中,得到:
![]()
解得:![]() ,
, ![]() 。
。
接下来,我们需要确定⊙C与线段AB有两个交点时,半径R的取值范围。
- 当⊙C与线段AB相切时,半径R最小,此时R等于点C到线段AB的距离。
- 当⊙C与线段AB相交时,半径R最大,此时R等于点C到线段AB的距离加上线段AB的一半。
点C到线段AB的距离可以通过垂线段公式计算得出:
![]() 。
。
因此,当⊙C与线段AB相切时,半径R最小为2。
当⊙C与线段AB相交时,半径R最大为点C到线段AB的距离加上线段AB的一半,即![]() 。
。
但是,由于⊙C是以点C为圆心,半径为R的圆,所以R的最大值不能超过AC或BC的长度,即R的最大值为√5。
综上所述,⊙C的半径R的取值范围是2 < R ≤ √5。
因此,正确答案是(A) 2 < R ≤ √5。
