2024届宝山区初三二模数学试卷精讲（第14题）

14. 如图，街心花园有 A、B、C 三座小亭子，A、C 两亭有坡地遮隔屏蔽，A、B、C 三亭所在处并不共线，设 AB、BC 的中点分别为 M、N，知其 MN = 3 米，测得 AC = ________ 米。

详细讲解

这是一个几何问题，涉及三角形的中位线定理。我们需要根据已知条件求解 AC 的长度。

解题步骤

1. 分析图形，应用中位线定理：
   在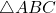 中，M 是 AB 的中点，N 是 BC 的中点，因此 MN 是三角形的中位线，平行于 AC，且满足：
   
2. 代入已知条件：
   已知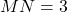 米，代入公式：
   
3. 解方程：
   两边同时乘以 2：
   
   因此， 米。
4. 检验：
   中位线定理适用于任何三角形，条件符合，计算无误。

最终答案：
AC = 6 米。

知识点复习与易错点扩展

1. 三角形中位线定理：
   在三角形中，连接两边中点的线段称为中位线。中位线平行于第三边，且长度为第三边的一半，即 。
2. 几何条件的理解：
   题目中提到 A、B、C 不共线，确保形成三角形；MN 是中位线，需正确识别其性质。
3. 易错点：
   – 误解中位线的定义，可能错认为 MN 平行于 AB 或 BC。
   – 计算时忘记将 MN 乘以 2 来求 AC，需注意中位线长度是第三边的一半。