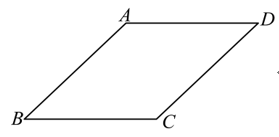
18. 如图,菱形ABCD的边长为5,\(\cos B = \frac{4}{5}\),E是边CD上一点(不与点C、D重合),把△ADE沿着直线AE翻折,如果点D落在菱形一边的延长线上,那么CE的长为________。
详细解答:
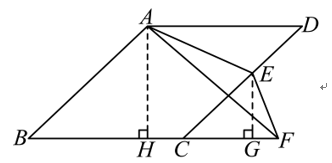
解:过点A作AH⊥BC于H,过点E作EG⊥CF于G,点D与点F重合,如图。
由折叠得:AF=AD=AB=5,
∴BH=AH,
∵\(\cos \angle B = \frac{4}{5}\),
∴BH=4,
∴BF=2BH=8,
∴FC=AF-AC=8-5=3,
∵四边形ABCD是菱形,
∴CD//AB,
∴∠DCF=∠B,
∵\(\cos \angle DCF = \cos \angle B = \frac{4}{5}\),
设CG=4y,则CE=5y,FG=CF-CG=3-4y,
在Rt△CEG中,由勾股定理得:\((3-4y)^2 + (3y)^2 = (5-5y)^2\),
解得:y=\(\frac{8}{13}\),
∴CE=5y=\(\frac{40}{13}\)。
还有第二个答案就是折在CD的延长线上形成等腰,简单计算可知答案是CE=1
相关知识点复习:
- 菱形的性质:对角线互相垂直平分,邻边相等。
- 勾股定理:直角三角形中,斜边的平方等于两直角边的平方和。
- 余弦函数:在直角三角形中,一个锐角的余弦值等于该角相邻边与斜边的比值。
易错提示和拓展:
- 在解题过程中,要注意区分不同的几何图形及其性质,正确运用勾股定理和余弦函数。
- 对于折叠问题,要理解折叠前后图形的位置关系,正确找出对应点。
- 解方程时,要注意检验解的合理性,确保解符合题意。
