题目:
23.如图10,在⊙O中,直径AB垂直于弦CD,垂足为点E。联结AC、DO,延长DO交AC于点F。
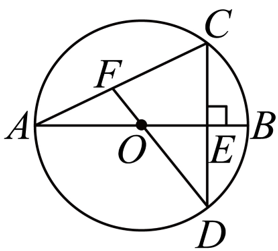
(1) 求证:AF=OF·DF;
(2) 如果CD=8,BE=2,求OF的长。
详细解答:
(1) 证明:连接AD
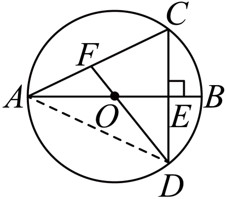
∵ 直径AB垂直于弦CD,
∴ CE = DE = \(\frac{1}{2}CD\),
∵ AE⊥CD,
∴ AC = AD,
∴ ∠FAO = ∠DAO,
∵ AO = DO,
∴ ∠DAO = ∠ODA,
∴ ∠FAO = ∠ODA,
又∠AFO = ∠DFA,
∴ △AFO∽△DFA,
∴ \(\frac{AF}{OF} = \frac{DF}{AF}\),
∴ AF² = OF·DF。
(2) 解答:
∵ CE = DE = \(\frac{1}{2}CD\),CD = 8,
∴ CE = DE = 4,
设半径为r,
∵ BE = 2,
∴ OE = r – 2,
在Rt△DEO中,OE² + DE² = DO²,
∴ (r – 2)² + 4² = r²,
解得r = 5,
∴ OE = 3,AE = AO + OE = 8,
∴ AD = \(\sqrt{AE² + DE²} = 4\sqrt{5}\),
∵ △AFO∽△DFA,
∴ \(\frac{AF}{DF} = \frac{OF}{AF} = \frac{AO}{AD}\),即 \(\frac{AF}{OF + 5} = \frac{OF}{4\sqrt{5}} = \frac{5}{4\sqrt{5}}\),
整理得 \(\begin{cases} 4\sqrt{5}OF = 5AF \\ 5OF + 25 = 4\sqrt{5}AF \end{cases}\),
解得 OF = \(\frac{25}{11}\)。
相关知识点复习:
1. 圆的性质:直径垂直于弦时,弦被平分。
2. 相似三角形的性质:对应边成比例。
3. 勾股定理的应用。
易错提示和拓展:
1. 在证明过程中,注意相似三角形的判定条件。
2. 解方程时,注意检查解的合理性。
3. 拓展:可以尝试其他方法证明AF = OF·DF,例如利用圆幂定理。
