题目:
24. 在平面直角坐标系xOy中(如图),已知开口向下的抛物线\(y = ax^2 – 2x + 4\)经过点\(P(0, 4)\),顶点为\(A\)。
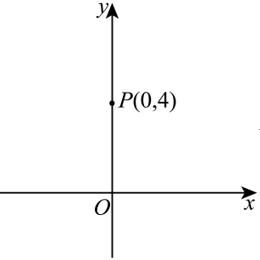
- 求直线\(PA\)的表达式。
- 如果将\(\triangle POA\)绕点\(O\)逆时针旋转90°,点\(A\)落在抛物线上的点\(Q\)处,求抛物线的表达式。
- 将(2)中得到的抛物线沿射线\(PA\)平移,平移后抛物线的顶点为\(B\),与y轴交于点\(C\)。如果\(PC = \sqrt{2}AB\),求\(\tan \angle PBC\)的值。
详细解答:
(1) 由\(y = ax^2 – 2x + 4 = a(x – \frac{1}{a})^2 + 4 – \frac{1}{a}\),可得\(A(\frac{1}{a}, 4 – \frac{1}{a})\)。
由题意设直线\(PA\)的表达式为\(y = kx + 4(k \neq 0)\)。
将\(A(\frac{1}{a}, 4 – \frac{1}{a})\)代入得:\(\frac{k}{a} + 4 = 4 – \frac{1}{a}\),解得\(k = -1\)。
所以,直线\(PA\)的表达式为\(y = -x + 4\)。
(2) 由抛物线开口向下且过点\(P(0, 4)\),\(\triangle POA\)绕点\(O\)逆时针旋转90°,点\(A\)的对应点\(Q\)在抛物线上。
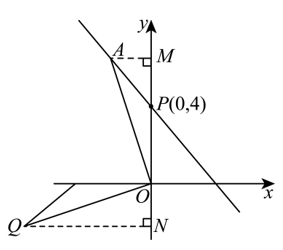
过点\(A\)、\(Q\)分别作\(AM \perp y\)轴,\(QN \perp y\)轴,垂足分别为点\(M\)、\(N\)。
于是\(\triangle OAM \cong \triangle QON\),则由\(A(\frac{1}{a}, 4 – \frac{1}{a})\)得\(Q(-\frac{1}{a}, 4 – \frac{1}{a})\)。
代入\(y = ax^2 – 2x + 4\)得\(8a^2 + 2a – 1 = 0\)。
解得\(a = -\frac{1}{2}\)或\(a = \frac{1}{4}\)(舍去)。
所以,\(a\)的值为\(\frac{1}{2}\)。
(3) 由(2)得\(y = \frac{1}{2}x^2 – 2x + 4 = \frac{1}{2}(x + 2)^2 + 6\),\(A(-2, 6)\)。
设平移后的抛物线表达式为\(y = \frac{1}{2}(x – m)^2 + 4 – m\)。
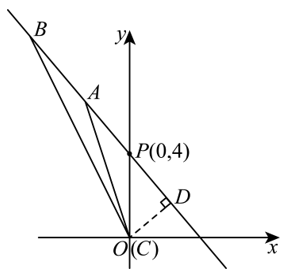
则\(B(m, 4 – m)\),\(C(0, \frac{1}{2}m^2 – m + 4)\)。
点\(B\)在点\(A\)的上方,点\(C\)在点\(P\)的下方。
于是,\(AB = \sqrt{(m + 2)^2 + (m + 2)^2} = \sqrt{2}|m + 2|\)。
\(PC = 4 – (\frac{1}{2}m^2 – m + 4) = \frac{1}{2}m^2 – m\)。
由\(PC = \sqrt{2}AB\),可得\(\frac{1}{2}m^2 – m = -2(m + 2)\)。
解得\(m = -4\)或\(m = -2\)(舍去)。
于是\(B(-4, 8)\),\(C(0, 0)\)。
在\(\triangle CDP\)中,\(\angle DPC = 45^\circ\),\(PC = 4\),可得\(CD = DP = 2\sqrt{2}\)。
\(BP = \sqrt{(0 + 4)^2 + (8 – 4)^2} = 4\sqrt{2}\),于是\(BD = DP + BP = 6\sqrt{2}\)。
所以,在\(\triangle CDB\)中,\(\tan \angle PBC = \frac{CD}{BD} = \frac{2\sqrt{2}}{6\sqrt{2}} = \frac{1}{3}\)。
相关知识点复习:
1. 抛物线的标准方程及其性质。
2. 直线的斜率和方程。
3. 平面几何中的旋转和平移变换。
易错提示和拓展:
1. 注意抛物线的开口方向和顶点坐标的关系。
2. 在进行几何变换时,注意点的坐标变化规律。
3. 解题过程中要注意代数运算的准确性。
