12. 某厂生产了 1000 只灯泡。为了解这 1000 只灯泡的使用寿命,从中随机抽取了 50 只灯泡进行检测,结果有 28 只灯泡的使用寿命超过了 2500 小时,那么估计这 1000 只灯泡中使用寿命超过 2500 小时的灯泡的数量为 ________ 只。
解析
题目解析
题目要求我们根据样本数据来估计总体中的某个特征的比例。这是一个典型的统计学问题,涉及到比例估计的知识点。
知识点复习
- 比例估计:在统计学中,当我们无法对整个总体进行测量时,通常会从总体中抽取一个样本,并用样本的比例来估计总体的比例。
- 样本比例:样本中具有某种特征的个体数与样本总数的比例。
- 总体比例:总体中具有某种特征的个体数与总体总数的比例。
解题步骤
- 确定样本比例:首先计算样本中使用寿命超过 2500 小时的灯泡的比例。
- 样本中使用寿命超过 2500 小时的灯泡数量为 28 只。
- 样本总数为 50 只。
- 样本比例 =
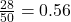
- 估计总体比例:假设样本比例可以代表总体比例,则总体中使用寿命超过 2500 小时的灯泡比例也为 0.56。
- 计算总体数量:最后,用总体比例乘以总体总数来估计总体中使用寿命超过 2500 小时的灯泡数量。
- 总体总数为 1000 只。
- 总体中使用寿命超过 2500 小时的灯泡数量 = 0.56 × 1000 = 560
易错点扩展
- 样本代表性:在实际应用中,样本必须具有代表性,否则样本比例可能不能准确反映总体比例。
- 样本大小:样本大小也会影响估计的准确性。一般来说,样本越大,估计越准确。
- 置信区间:为了更精确地估计总体比例,可以使用置信区间的方法,给出一个估计范围而不是单一数值。
