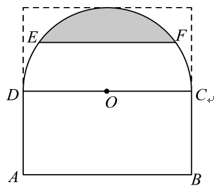
16. 为传承海派文化,社区准备举办沪剧爱好者观摩演出活动.把某场馆的一个正方形区域改造成一个由矩形和半圆形组成的活动场地(如图),矩形是观众观演区,阴影部分是舞台,是半圆 O 的直径,弦与平行.已知长 8 米,舞台区域最大深度为 2 米,如果每平方米最多可以坐 3 名观众,那么观演区可容纳 __________ 名观众.
1. 题目分析
题目描述了一个正方形区域被改造成由矩形和半圆形组成的活动场地。矩形部分是观众观演区,阴影部分是舞台(半圆)。已知:
- 弦 \( EF \) 的长度为 8 米,且与正方形的一边 \( AB \) 平行。
- 舞台区域的最大深度为 2 米(即半圆的半径减去弦 \( EF \) 到圆心的垂直距离)。
- 每平方米最多可以坐 3 名观众。
目标是计算观演区(矩形区域)可以容纳多少名观众。
2. 解题步骤
第一步:画图并标注已知条件
- 正方形区域的一条边为 \( AB \),设其长度为 \( s \)。
- 半圆 \( O \) 的直径是 \( AB \),因此半圆的半径 \( r = \frac{s}{2} \)。
- 弦 \( EF \) 与 \( AB \) 平行,且 \( EF = 8 \) 米。
- 舞台的最大深度为 2 米,即 \( HG = 2 \) 米。
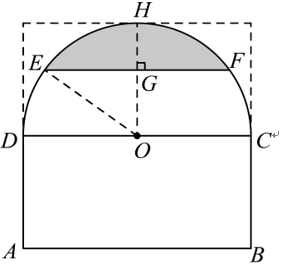
第二步:作辅助线
按照题目要求,作辅助线:
- 过 \( O \) 作 \( OG \perp EF \) 于 \( G \),交弧于 \( H \),连接 \( OE \)。
- 因为 \( OG \perp EF \),所以 \( G \) 是 \( EF \) 的中点,\( EG = \frac{1}{2} EF = 4 \) 米。
- 舞台的最大深度为 2 米,即 \( HG = 2 \) 米,因此 \( OG = OH – HG = r – 2 \)。
第三步:利用勾股定理求半径
在直角三角形 \( OEG \) 中:
- \( OE = r \)(半径)。
- \( EG = 4 \) 米。
- \( OG = r – 2 \) 米。
根据勾股定理:
\[
OE^2 = EG^2 + OG^2
\]
\[
r^2 = 4^2 + (r – 2)^2
\]
\[
r^2 = 16 + r^2 – 4r + 4
\]
\[
0 = 20 – 4r
\]
\[
4r = 20
\]
\[
r = 5 \text{ 米}
\]
因此,半圆的半径 \( r = 5 \) 米。
第四步:确定正方形的边长
半圆的直径 \( AB = 2r = 10 \) 米,因此正方形的边长 \( AB = 10 \) 米。
第五步:确定矩形的尺寸
矩形 \( ABCD \) 的边:
- \( AB = 10 \) 米(与半圆直径重合)。
- \( BC = AB – r = 10 – 5 = 5 \) 米(因为半圆的半径为 5 米,占据了一半的正方形边长)。
因此,矩形 \( ABCD \) 的面积为:
\[
\text{面积} = AB \times BC = 10 \times 5 = 50 \text{ 平方米}
\]
第六步:计算观众人数
每平方米最多可以坐 3 名观众:
\[
\text{观众人数} = 50 \times 3 = 150 \text{ 人}
\]
3. 知识点
- 圆的性质:
- 半径:从圆心到圆上任意一点的距离,在本题中为 \( r = 5 \) 米。
- 直径:通过圆心且两端在圆上的线段,长度为 \( 2r \),在本题中为 \( AB = 10 \) 米。
- 弦:连接圆上任意两点的线段,如 \( EF = 8 \) 米。
- 垂径定理:垂直于弦的直径平分该弦及其所对的弧,在本题中 \( OG \perp EF \),平分 \( EF \),使 \( EG = 4 \) 米。
- 勾股定理:
- 在直角三角形中,两直角边的平方和等于斜边的平方,即 \( a^2 + b^2 = c^2 \)。
- 在本题中,应用于 \( \triangle OEG \):\( OE^2 = EG^2 + OG^2 \),解出半径 \( r = 5 \) 米。
- 矩形和半圆的面积计算:
- 矩形面积公式:\( \text{面积} = 长 \times 宽 \),在本题中为 \( 10 \times 5 = 50 \) 平方米。
- 半圆面积公式:\( \text{面积} = \frac{1}{2} \pi r^2 \),虽未直接使用,但理解其与矩形的关系有助于建模。
- 实际问题的数学建模:
- 将现实场景(如场地改造)转化为几何图形(正方形、矩形、半圆)。
- 通过条件(如最大深度、弦长)建立方程,求解未知量(如半径、面积)。
- 结合单位换算(如每平方米 3 人)得出最终结果。
4. 易错点和拓展
易错点:
- 图形理解错误:
- 误以为半圆的直径不是正方形的边,或弦 \( EF \) 不平行于 \( AB \),导致位置关系混乱。
- 建议:仔细读题,结合图示明确矩形和半圆的相对位置。
- 最大深度的误解:
- 未理解“最大深度”是指 \( HG = 2 \) 米,即半径与弦到圆心距离的差,误以为是其他距离。
- 建议:在图中标注 \( HG \) 和 \( OG \),明确其与半径的关系。
- 勾股定理应用错误:
- 在 \( \triangle OEG \) 中,误将 \( OG \) 或 \( EG \) 的值代入,导致方程错误。
- 建议:列方程前检查三角形各边的定义,确保 \( OE = r \)、\( EG = 4 \)、\( OG = r – 2 \)。
- 观众人数计算失误:
- 忘记乘以每平方米的观众数(3 人),或对面积取整后计算。
- 建议:分步计算,先求面积,再乘以人数密度,最后检查单位是否一致。
拓展:
- 改变舞台形状:
- 若舞台改为扇形(如半圆的 1/4),面积变为 \( \frac{1}{4} \pi r^2 \),重新计算观演区面积。
- 若舞台为弓形(弦 \( EF \) 与弧围成),可用公式 \( \text{弓形面积} = \frac{1}{2} r^2 (\theta – \sin\theta) \)(\(\theta\) 为圆心角),探索面积变化。
- 不同布局的面积关系:
- 若半圆位置移至正方形另一边,矩形尺寸会变(如长 10 米,宽 3 米),比较不同布局的观众容量。
- 思考:哪种布局能容纳更多观众?是否存在最优解?
- 引入实际限制条件:
- 考虑安全距离:若观众区需留 1 米通道,矩形宽减为 4 米,面积变为 \( 10 \times 4 = 40 \) 平方米,容纳 \( 40 \times 3 = 120 \) 人。
- 考虑座位排列:若每人占 0.5 平方米,重新计算实际人数(\( 50 \div 0.5 = 100 \) 人)。
- 动态调整参数:
- 若弦长 \( EF \) 变为 6 米,最大深度仍为 2 米,重新计算 \( r \) 和面积,观察观众人数变化。
- 问题:弦长与观众人数的关系是线性的吗?尝试推导。
最终答案
观演区可容纳 \(\boxed{150}\) 名观众。
