题目:
21. 如图,在平面直角坐标系xOy中,直线 \(y = x + 3\) 与x轴、y轴分别交于点A、B,与反比例函数 \(y = \frac{k}{x}\) 的图像交于点C(2, m).
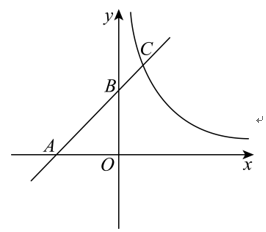
- (1)求反比例函数的解析式;
- (2)过点C作x轴的平行线l,如果点D在直线l上,且CD = 3,求△ABD的面积.
详细解答:
(1)解:在 \(y = x + 3\) 中,当 \(x = 2\) 时,\(y = x + 3 = 2 + 3 = 5\)。
∴ C(2, 5)。
把C(2, 5)代入 \(y = \frac{k}{x}\) 中得,\(5 = \frac{k}{2}\)。
∴ \(k = 10\)。
∴ 反比例函数解析式为 \(y = \frac{10}{x}\)。
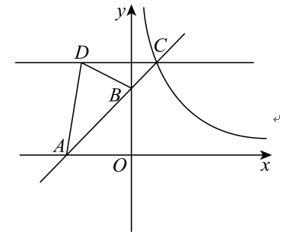
(2)解:∵ 直线 \(y = x + 3\) 与x轴、y轴分别交于点A、B。
∴ A(-3, 0),B(0, 3)。
∴ \(S_{\triangle ABD} = S_{\triangle ACD} – S_{\triangle BCD}\)。
\(= \frac{1}{2} \times 3 \times 5 – \frac{1}{2} \times 3 \times (5 – 3)\)
\(= \frac{9}{2}\)
相关知识点复习:
- 直线方程的求解方法:通过已知条件确定直线上的两点,利用两点式或斜截式求解直线方程。
- 反比例函数的性质:反比例函数 \(y = \frac{k}{x}\) 中,\(k\) 为常数,当 \(x\) 增大时,\(y\) 减小;当 \(x\) 减小时,\(y\) 增大。
- 平行线的性质:平行线间的距离相等。
- 三角形面积的计算方法:利用底和高的乘积的一半来计算。
易错提示和拓展:
- 在求解反比例函数解析式时,注意将已知点的坐标代入公式求解 \(k\) 值。
- 在计算三角形面积时,注意选择合适的底和高进行计算。
- 拓展:可以进一步探讨直线与反比例函数图像的交点个数问题。
