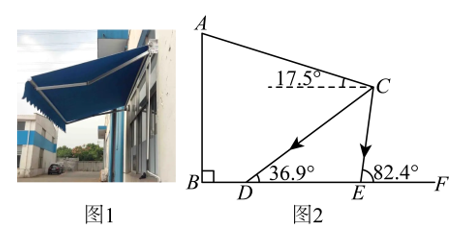
题目:小明家院内靠墙安装了一个遮阳篷(如图1),图2是它的侧面示意图,遮阳篷长AC=6米,与水平面的夹角为17.5°,靠墙端A离地高度AB=5米,已知该地区冬至正午太阳光照入射角∠CDF=36.9°,夏至正午太阳光照入射角∠CEF=82.4°。因此,点D、E之间的区域是一年四季中阳光不一定照射到的区域。求该区域深度DE的长。(结果精确到0.1米)参考数据:sin17.5°≈0.3, cos17.5°≈0.95, tan17.5°≈0.32;sin36.9°≈0.6, cos36.9°≈0.8, tan36.9°≈0.75;sin82.4°≈0.99, cos82.4°≈0.13, tan82.4°≈7.5。
详细解答:
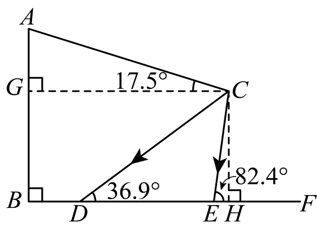
解:过C作CG⊥AB于G,CH⊥DE于H。
根据题意知∠B=90°。
∴四边形CGBH是矩形。
∴CH=BG。
在Rt△ACG中,AG=AC·sin∠ACG=6×sin17.5°=6×0.3=1.8。
又AB=5,
∴CH=BG=AB−AG=3.2。
在Rt△CEH中,EH= \(\frac{CH}{tan∠CEH}\)=\(\frac{3.2}{tan82.4°}\)≈\(\frac{3.2}{7.5}\)≈0.43。
在Rt△CDH中,DH= \(\frac{CH}{tan∠CDH}\)=\(\frac{3.2}{tan36.9°}\)≈\(\frac{3.2}{0.75}\)≈4.27。
∴DE=DH−EH=4.27−0.43≈3.8。
答:该区域深度DE的长为3.8米。
相关知识点复习:
1. 直角三角形的基本性质及其应用。
2. 正弦、余弦、正切函数的定义及应用。
3. 解直角三角形的方法。
易错提示和拓展:
1. 在解题过程中要注意角度的单位,确保使用正确的三角函数值。
2. 在计算过程中要保留足够的有效数字,以保证最终结果的准确性。
3. 可以进一步探讨不同季节太阳光照入射角的变化对遮阳篷阴影区域的影响。
