题目:
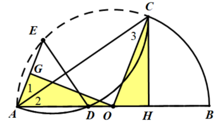
25. 已知 \(AB\) 是半圆 \(O\) 的直径,\(C\) 是半圆 \(O\) 上不与 \(A\)、\(B\) 重合的点,将弧 \(AC\) 沿直线 \(AC\) 翻折,翻折所得的弧交直径 \(AB\) 于点 \(D\),\(E\) 是点 \(D\) 关于直线 \(AC\) 的对称点。
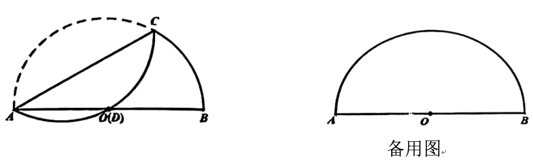
(1) 如图,点 \(D\) 恰好落在点 \(O\) 处。
用尺规作图在图中作出点 \(E\)(保留作图痕迹),连接 \(AE\)、\(CE\)、\(CD\),求证:四边形 \(ADCE\) 是菱形;
连接 \(BE\),与 \(AC\)、\(CD\) 分别交于点 \(F\)、\(G\),求 \(\frac{FG}{BE}\) 的值;
(2) 如果 \(AB=10, OD=1\),求折痕 \(AC\) 的长。
详细解答:
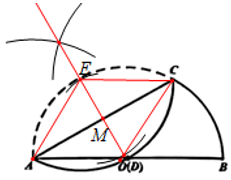
(1) 证明:\(E\) 是点 \(D\) 关于直线 \(AC\) 的对称点。
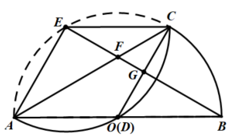
\(AE = AD\), \(CE = CD\)。
\(AD = CD\)。
\(AE = AD = CE = CD\)。
四边形 \(ADCE\) 是菱形。
\(CE \parallel AD\)。
\(\frac{CF}{AF} = \frac{CE}{AB} = \frac{1}{2}\)。
\(FG = \frac{1}{3} EG\), \(EG = \frac{1}{2} BE\)。
\(FG = \frac{1}{6} BE\), \(\frac{FG}{BE} = \frac{1}{6}\)。
(2) 当点 \(D\) 在点 \(O\) 右侧。
作点 \(D\) 关于直线 \(AC\) 的对称点 \(E\),联结 \(DE\)、\(AE\)。
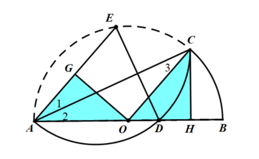
过点 \(O\) 作 \(OG \perp AE\),垂足为点 \(G\)。过点 \(C\) 作 \(CH \perp AB\),垂足为点 \(H\)。
\(\angle AGO = \angle OHC = 90^\circ\)。
\(AE = AD\), \(DE \perp AC\), \(\angle 1 = \angle 2\)。
\(AO = CO\), \(\angle = \angle 2\)。
\(\angle COH = \angle 2 + \angle 3 = 2 \angle 2\)。
\(\angle OAG = \angle 1 + \angle 2 = 2 \angle 2\)。
\(\angle COH = \angle OAG\)。
\(AO = CO\), \(\triangle OAG \cong \triangle COH\), \(AG = OH\)。
\(AB = 10\), \(OD = 1\), \(AD = AE = 6\)。
\(OG \perp AE\), \(AG = \frac{1}{2} AE = 3\)。
\(OH = 3\), \(AH = 8\)。
在 \(Rt\triangle COH\) 中, \(CH = \sqrt{CO^2 – OH^2} = \sqrt{5^2 – 3^2} = 4\)。
在 \(Rt\triangle ACH\) 中, \(AC = \sqrt{AH^2 + CH^2} = \sqrt{8^2 + 4^2} = 4\sqrt{5}\)。
当点 \(D\) 在点 \(O\) 左侧,同理可得 \(AC = \sqrt{70}\)。
综上所述:折痕 \(AC\) 的长为 \(4\sqrt{5}\) 或者 \(\sqrt{70}\)。
相关知识点复习:
1. 菱形的性质:对角线互相垂直平分,四边相等。
2. 直角三角形的勾股定理:直角三角形两直角边的平方和等于斜边的平方。
3. 对称性:点关于直线的对称点到直线的距离相等。
易错提示和拓展:
1. 注意区分点 \(D\) 在点 \(O\) 右侧和左侧的情况,不同的位置会导致不同的结果。
2. 在解题过程中,要充分利用几何图形的对称性和直角三角形的性质。
3. 解题时要注意细节,如点 \(D\) 的位置变化对结果的影响。
